to BIPM.org
CIPM MRA PARTICIPANTS
All data listed in the KCDB have been reviewed and approved within the CIPM Mutual Recognition Arrangement
Menu
Login
CIPM MRA PARTICIPANTS
CMC statistics
Comparison
Comparison close
Results
print out

EUROMET.T-K3, EURAMET.T-K3.3, EURAMET.T-K3.1 and EURAMET.T-K3.5

NOMINAL TEMPERATURE : Mercury Triple Point, 234.3156 K

Degrees of equivalence, Di and expanded uncertainty Ui (k = 2),
both expressed in mK

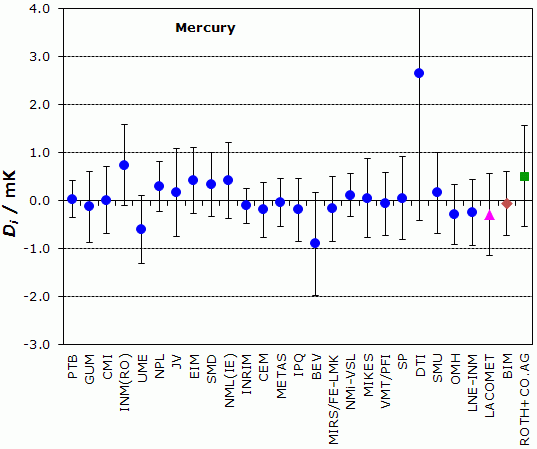
Blue circles: participants in EUROMET.T-K3
Pink triangle: participant in EURAMET.T-K3.3 only
Brown diamond: participant in EURAMET.T-K3.1 only
Green square: participant in EURAMET.T-K3.5 only

print out

EUROMET.T-K3, EURAMET.T-K3.3, EURAMET.T-K3.1 and EURAMET.T-K3.5

NOMINAL TEMPERATURE : Gallium Melting Point, 302.9146 K

Degrees of equivalence, Di and expanded uncertainty Ui (k = 2),
both expressed in mK

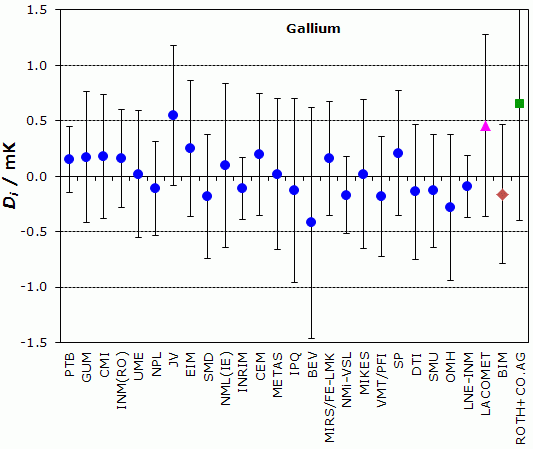
Blue circles: participants in EUROMET.T-K3
Pink triangle: participant in EURAMET.T-K3.3 only
Brown diamond: participant in EURAMET.T-K3.1 only
Green square: participant in EURAMET.T-K3.5 only

print out

EUROMET.T-K3, EURAMET.T-K3.3, EURAMET.T-K3.1 and EURAMET.T-K3.5

NOMINAL TEMPERATURE : Indium Freezing Point, 429.7485 K

Degrees of equivalence, Di and expanded uncertainty Ui (k = 2),
both expressed in mK

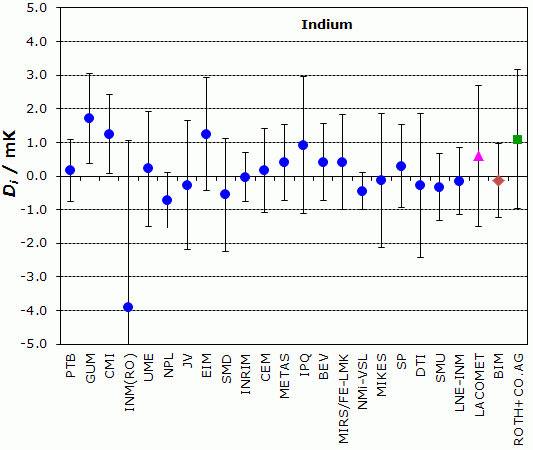
Blue circles: participants in EUROMET.T-K3
Pink triangle: participant in EURAMET.T-K3.3 only
Brown diamond: participant in EURAMET.T-K3.1 only
Green square: participant in EURAMET.T-K3.5 only

print out

EUROMET.T-K3, EURAMET.T-K3.3, EURAMET.T-K3.1 and EURAMET.T-K3.5

NOMINAL TEMPERATURE : Tin Freezing Point, 505.078 K

Degrees of equivalence, Di and expanded uncertainty Ui (k = 2),
both expressed in mK

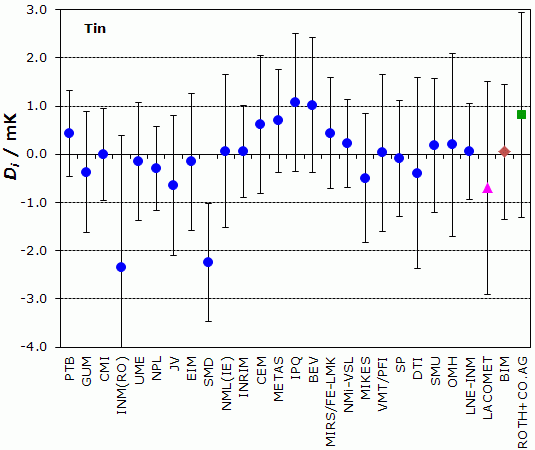
Blue circles: participants in EUROMET.T-K3
Pink triangle: participant in EURAMET.T-K3.3 only
Brown diamond: participant in EURAMET.T-K3.1 only
Green square: participant in EURAMET.T-K3.5 only

print out

EUROMET.T-K3, EURAMET.T-K3.3, EURAMET.T-K3.1 and EURAMET.T-K3.5

NOMINAL TEMPERATURE : Zinc Freezing Point, 692.677 K

Degrees of equivalence, Di and expanded uncertainty Ui (k = 2),
both expressed in mK

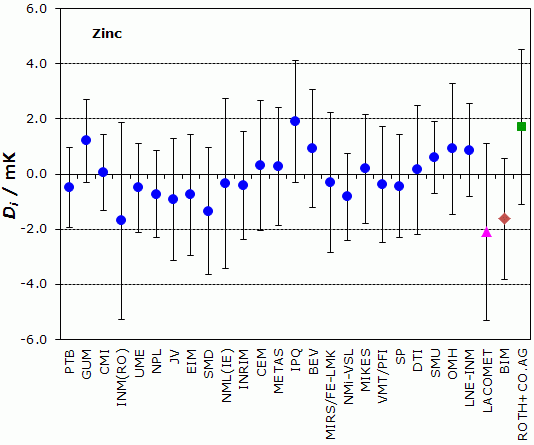
Blue circles: participants in EUROMET.T-K3
Pink triangle: participant in EURAMET.T-K3.3 only
Brown diamond: participant in EURAMET.T-K3.1 only
Green square: participant in EURAMET.T-K3.5 only

Comparison
Comparison close
Results
print out

EUROMET.T-K3, EURAMET.T-K3.3, EURAMET.T-K3.1 and EURAMET.T-K3.5

NOMINAL TEMPERATURE : Mercury Triple Point, 234.3156 K

All values given in the following Table are expressed in mK

   
Lab iDiUi
PTB 0.030.39
GUM-0.130.74
CMI0.010.70
INM(RO)0.740.84
UME-0.610.71
NPL0.300.52
JV0.170.91
EIM0.420.69
SMD0.340.67
NML(IE)0.420.80
INRIM-0.110.37
CEM-0.190.57
METAS-0.040.51
IPQ-0.190.66
BEV-0.901.07
MIRS/FE-LMK-0.170.68
NMi-VSL0.110.45
MIKES0.050.82
VMT/PFI-0.070.65
SP0.050.87
DTI2.663.08
SMU0.160.84
OMH-0.290.63
LNE-INM-0.250.68

LACOMET: participant in EURAMET.T-K3.3 only
DLACOMET = -0.29 mK and ULACOMET = 0.85 mK

BIM: participant in EURAMET.T-K3.1 only
DBIM = -0.06 mK and UBIM = 0.67 mK

ROTH+CO.AG: participant in EURAMET.T-K3.5 only
DROTH+CO.AG = 0.51 mK and UROTH+CO.AG = 1.06 mK

Results are presented under A4 printable format in Summary Results (PDF file).

print out

EUROMET.T-K3, EURAMET.T-K3.3, EURAMET.T-K3.1 and EURAMET.T-K3.5

NOMINAL TEMPERATURE : Gallium Melting Point, 302.9146 K

All values given in the following Table are expressed in mK

   
Lab iDiUi
PTB 0.150.30
GUM0.170.59
CMI0.180.56
INM(RO)0.160.44
UME0.020.57
NPL-0.110.42
JV0.550.63
EIM0.250.61
SMD-0.180.56
NML(IE)0.100.74
INRIM-0.110.28
CEM0.200.55
METAS0.020.68
IPQ-0.130.83
BEV-0.421.04
MIRS/FE-LMK0.160.51
NMi-VSL-0.170.35
MIKES0.020.67
VMT/PFI-0.180.54
SP0.210.56
DTI-0.140.61
SMU-0.130.51
OMH-0.280.66
LNE-INM-0.090.28

LACOMET: participant in EURAMET.T-K3.3 only
DLACOMET = 0.46 mK and ULACOMET = 0.82 mK

BIM: participant in EURAMET.T-K3.1 only
DBIM = -0.16 mK and UBIM = 0.63 mK

ROTH+CO.AG: participant in EURAMET.T-K3.5 only
DROTH+CO.AG = 0.66 mK and UROTH+CO.AG = 1.06 mK

Results are presented under A4 printable format in Summary Results (PDF file).

print out

EUROMET.T-K3, EURAMET.T-K3.3, EURAMET.T-K3.1 and EURAMET.T-K3.5

NOMINAL TEMPERATURE : Indium Freezing Point, 429.7485 K

All values given in the following Table are expressed in mK

   
Lab iDiUi
PTB 0.160.92
GUM1.711.35
CMI1.241.18
INM(RO)-3.904.95
UME0.221.71
NPL-0.730.83
JV-0.281.92
EIM1.251.68
SMD-0.561.68
INRIM-0.030.72
CEM0.171.25
METAS0.401.12
IPQ0.922.03
BEV0.411.15
MIRS/FE-LMK0.411.41
NMi-VSL-0.450.56
MIKES-0.141.99
SP0.291.24
DTI-0.292.14
SMU-0.330.99
LNE-INM-0.150.99

LACOMET: participant in EURAMET.T-K3.3 only
DLACOMET = 0.6 mK and ULACOMET = 2.1 mK

BIM: participant in EURAMET.T-K3.1 only
DBIM = -0.14 mK and UBIM = 1.1 mK

ROTH+CO.AG: participant in EURAMET.T-K3.5 only
DROTH+CO.AG = 1.09 mK and UROTH+CO.AG = 2.07 mK

Results are presented under A4 printable format in Summary Results (PDF file).

print out

EUROMET.T-K3, EURAMET.T-K3.3, EURAMET.T-K3.1 and EURAMET.T-K3.5

NOMINAL TEMPERATURE : Tin Freezing Point, 505.078 K

All values given in the following Table are expressed in mK

   
Lab iDiUi
PTB 0.430.90
GUM-0.371.26
CMI0.000.95
INM(RO)-2.342.72
UME-0.151.22
NPL-0.290.87
JV-0.651.45
EIM-0.161.42
SMD-2.241.22
NML(IE)0.061.59
INRIM0.060.95
CEM0.611.43
METAS0.691.07
IPQ1.071.43
BEV1.021.40
MIRS/FE-LMK0.441.15
NMi-VSL0.220.92
MIKES-0.501.34
VMT/PFI0.031.63
SP-0.091.20
DTI-0.391.98
SMU0.181.39
OMH0.201.90
LNE-INM0.061.00

LACOMET: participant in EURAMET.T-K3.3 only
DLACOMET = -0.7 mK and ULACOMET = 2.2 mK

BIM: participant in EURAMET.T-K3.1 only
DBIM = 0.05 mK and UBIM = 1.4 mK

ROTH+CO.AG: participant in EURAMET.T-K3.5 only
DROTH+CO.AG = 0.82 mK and UROTH+CO.AG = 2.13 mK

Results are presented under A4 printable format in Summary Results (PDF file).

print out

EUROMET.T-K3, EURAMET.T-K3.3, EURAMET.T-K3.1 and EURAMET.T-K3.5

NOMINAL TEMPERATURE : Zinc Freezing Point, 692.677 K

All values given in the following Table are expressed in mK

   
Lab iDiUi
PTB -0.491.44
GUM1.211.51
CMI0.071.38
INM(RO)-1.703.57
UME-0.501.61
NPL-0.731.57
JV-0.922.21
EIM-0.752.20
SMD-1.352.31
NML(IE)-0.343.09
INRIM-0.431.96
CEM0.302.36
METAS0.272.13
IPQ1.922.21
BEV0.922.13
MIRS/FE-LMK-0.302.54
NMi-VSL-0.821.58
MIKES0.191.98
VMT/PFI-0.372.11
SP-0.441.87
DTI0.162.34
SMU0.601.32
OMH0.912.39
LNE-INM0.861.69

LACOMET: participant in EURAMET.T-K3.3 only
DLACOMET = -2.1 mK and ULACOMET = 3.2 mK

BIM: participant in EURAMET.T-K3.3 only
DBIM = -1.62 mK and UBIM = 2.2 mK

ROTH+CO.AG: participant in EURAMET.T-K3.5 only
DROTH+CO.AG = 1.72 mK and UROTH+CO.AG = 2.82 mK

Results are presented under A4 printable format in Summary Results (PDF file).

Comparison
Comparison close
RMO comparison
Linked comparison
EURAMET.T-K3.1
print out
Metrology area, Sub-field Thermometry, Standard Platinum Resistance Thermometers
Description Realizations of the ITS-90 from 234.3 K to 692.7 K
Time of measurements 2008 - 2009
Status Approved for equivalence
Final Reports of the comparisons
EURAMET.T-K3.1 Final Report, 2012, 45 pages
Metrologia, 2013, 50, Tech. Suppl., 03002
Measurand Temperature: 234.3 K to 692.7 K
Transfer device Standard Platinum Resistance Thermometers
Comparison type Key Comparison
Consultative Committee CCT (Consultative Committee for Thermometry)
Conducted by EURAMET (European Association of National Metrology Institutes)
Comments

This comparison is organized and funded within the framework of PHARE project BG 2005/017-353.02.02, LOT 1.

Results published on 07 February 2013

EURAMET.T-K3.3, EURAMET.T-K3.1 and EURAMET.T-K3.5 results are linked to those of EUROMET.T-K3

Realizations of the ITS-90 from 234.3156 K to 692.677 K
Pilot institute BIM
Bulgarian Institute of Metrology
Bulgaria
Contact person Sasho NEDIALKOV

+359 2 8762 946
First Name Last Name
wwww@ww.www +356719836 Institute 1 Institute 1 Khmelnitskiy
Pilot laboratory
BIM

Bulgarian Institute of Metrology, Bulgaria, EURAMET

VSL

VSL, Netherlands, EURAMET

Comparison
Comparison close
Results
print out

EUROMET.T-K3, EURAMET.T-K3.3, EURAMET.T-K3.1 and EURAMET.T-K3.5

NOMINAL TEMPERATURE : Mercury Triple Point, 234.3156 K

  • Key comparison EUROMET.T-K3

For each fixed-point temperature, the difference (TR - TP) between the EUROMET reference value, TR, and TP, is computed as the weighted mean of all participants' results (Ti - TP), with weights inversely proportional to uiP, as explained in Section 8.1 of the Final Report.

For each fixed-point temperature, the degree of equivalence of laboratory i with respect to the EUROMET reference value is given by a pair of terms, both expressed in mK: Di = (Ti - TR), obtained from the differences relative to the Pilot Laboratory
Di = (Ti - TP) - (TR - TP), and Ui, its expanded uncertainty (k = 2), involving the measurement uncertainty at laboratory i, the uncertainty associated with the stability of the travelling SPRTs, and the repeatability of the calibration at the Pilot Laboratory (see Section 8.2 of the Final Report).
For each fixed-point temperature, the degree of equivalence between two laboratories i and j is given by a pair of terms, both expressed in mK: Dij = Di - Dj, and Uij, its expanded uncertainty at a 95 % level of confidence. The computation of Uij between participants in the same loop, and participants in different loops is explained in Sections 11.1 and 11.2 of the Final Report.
  • Linking EUROMET.T-K3 to CCT-K3

The Pilot Laboratory and the five Co-Pilots have participated in both comparisons.
The comparison of their averaged results in both exercises shows that they perform equally within 0.1 mK for all temperatures, except for the Zinc fixed-point temperature (0.23 mK) and the Tin fixed-point temperature (0.14 mK), as explained in Section 10.1 of the Final Report.
The uncertainty linked with the reproducibility between both exercises in also computed (see Table 28 on page 60 of the Final Report) and taken into account for the estimation of the pair-wise degrees of equivalence between participants in EUROMET.T-K3 and CCT-K3 (see Section 11.3 of the Final Report).

For each fixed-point temperature, the BIPM key comparison database displays the degrees of equivalence relative to the EUROMET reference value, and the pair-wise degrees of equivalence computed inside the EUROMET key comparison.

  • Linking EURAMET.T-K3.3, EURAMET.T-K3.1 and EURAMET.T-K3.5 to EUROMET.T-K3 and CCT-K3

The LACOMET results obtained in EURAMET.T-K3.3 are linked to the results of EUROMET.T-K3 and CCT-K3 using the participation of CEM in EUROMET.T-K3, whose results are linked to those of CCT-K3, as described above.
The BIM results obtained in EURAMET.T-K3.1 are linked to the results of EUROMET.T-K3 and CCT-K3 using the participation of VSL in EUROMET.T-K3.
The ROTH+CO.AG results obtained in EURAMET.T-K3.5 are linked to the results of EUROMET.T-K3 and CCT-K3 using the participation of VSL in EUROMET.T-K3.
This makes it possible to extend the EUROMET.T-K3 graphs of equivalence with LACOMET, BIM and ROTH+CO.AG results.
LACOMET and BIM degrees of equivalence relative to the CCT-K3 ARV are given on page 17 of the EURAMET.T-K3.3 Final Report and on pages 10 and 11 of the EURAMET.T-K3.1 Final Report, respectively.
The computation of ROTH+CO.AG degrees of equivalence relative to the CCT-K3 ARV is explained in Section 8.1 of the EURAMET.T-K3.5 Final Report.

print out

EUROMET.T-K3, EURAMET.T-K3.3, EURAMET.T-K3.1 and EURAMET.T-K3.5

NOMINAL TEMPERATURE : Gallium Melting Point, 302.9146 K

  • Key comparison EUROMET.T-K3

For each fixed-point temperature, the difference (TR - TP) between the EUROMET reference value, TR, and TP, is computed as the weighted mean of all participants' results (Ti - TP), with weights inversely proportional to uiP, as explained in Section 8.1 of the Final Report.

For each fixed-point temperature, the degree of equivalence of laboratory i with respect to the EUROMET reference value is given by a pair of terms, both expressed in mK: Di = (Ti - TR), obtained from the differences relative to the Pilot Laboratory
Di = (Ti - TP) - (TR - TP), and Ui, its expanded uncertainty (k = 2), involving the measurement uncertainty at laboratory i, the uncertainty associated with the stability of the travelling SPRTs, and the repeatability of the calibration at the Pilot Laboratory (see Section 8.2 of the Final Report).
For each fixed-point temperature, the degree of equivalence between two laboratories i and j is given by a pair of terms, both expressed in mK: Dij = Di - Dj, and Uij, its expanded uncertainty at a 95 % level of confidence. The computation of Uij between participants in the same loop, and participants in different loops is explained in Sections 11.1 and 11.2 of the Final Report.
  • Linking EUROMET.T-K3 to CCT-K3

The Pilot Laboratory and the five Co-Pilots have participated in both comparisons.
The comparison of their averaged results in both exercises shows that they perform equally within 0.1 mK for all temperatures, except for the Zinc fixed-point temperature (0.23 mK) and the Tin fixed-point temperature (0.14 mK), as explained in Section 10.1 of the Final Report.
The uncertainty linked with the reproducibility between both exercises in also computed (see Table 28 on page 60 of the Final Report) and taken into account for the estimation of the pair-wise degrees of equivalence between participants in EUROMET.T-K3 and CCT-K3 (see Section 11.3 of the Final Report).

For each fixed-point temperature, the BIPM key comparison database displays the degrees of equivalence relative to the EUROMET reference value, and the pair-wise degrees of equivalence computed inside the EUROMET key comparison.

  • Linking EURAMET.T-K3.3, EURAMET.T-K3.1 and EURAMET.T-K3.5 to EUROMET.T-K3 and CCT-K3

The LACOMET results obtained in EURAMET.T-K3.3 are linked to the results of EUROMET.T-K3 and CCT-K3 using the participation of CEM in EUROMET.T-K3, whose results are linked to those of CCT-K3, as described above.
The BIM results obtained in EURAMET.T-K3.1 are linked to the results of EUROMET.T-K3 and CCT-K3 using the participation of VSL in EUROMET.T-K3.
The ROTH+CO.AG results obtained in EURAMET.T-K3.5 are linked to the results of EUROMET.T-K3 and CCT-K3 using the participation of VSL in EUROMET.T-K3.
This makes it possible to extend the EUROMET.T-K3 graphs of equivalence with LACOMET, BIM and ROTH+CO.AG results.
LACOMET and BIM degrees of equivalence relative to the CCT-K3 ARV are given on page 17 of the EURAMET.T-K3.3 Final Report and on pages 10 and 11 of the EURAMET.T-K3.1 Final Report, respectively.
The computation of ROTH+CO.AG degrees of equivalence relative to the CCT-K3 ARV is explained in Section 8.1 of the EURAMET.T-K3.5 Final Report.

print out

EUROMET.T-K3, EURAMET.T-K3.3, EURAMET.T-K3.1 and EURAMET.T-K3.5

NOMINAL TEMPERATURE : Indium Freezing Point, 429.7485 K

  • Key comparison EUROMET.T-K3

For each fixed-point temperature, the difference (TR - TP) between the EUROMET reference value, TR, and TP, is computed as the weighted mean of all participants' results (Ti - TP), with weights inversely proportional to uiP, as explained in Section 8.1 of the Final Report.

For each fixed-point temperature, the degree of equivalence of laboratory i with respect to the EUROMET reference value is given by a pair of terms, both expressed in mK: Di = (Ti - TR), obtained from the differences relative to the Pilot Laboratory
Di = (Ti - TP) - (TR - TP), and Ui, its expanded uncertainty (k = 2), involving the measurement uncertainty at laboratory i, the uncertainty associated with the stability of the travelling SPRTs, and the repeatability of the calibration at the Pilot Laboratory (see Section 8.2 of the Final Report).
For each fixed-point temperature, the degree of equivalence between two laboratories i and j is given by a pair of terms, both expressed in mK: Dij = Di - Dj, and Uij, its expanded uncertainty at a 95 % level of confidence. The computation of Uij between participants in the same loop, and participants in different loops is explained in Sections 11.1 and 11.2 of the Final Report.
  • Linking EUROMET.T-K3 to CCT-K3

The Pilot Laboratory and the five Co-Pilots have participated in both comparisons.
The comparison of their averaged results in both exercises shows that they perform equally within 0.1 mK for all temperatures, except for the Zinc fixed-point temperature (0.23 mK) and the Tin fixed-point temperature (0.14 mK), as explained in Section 10.1 of the Final Report.
The uncertainty linked with the reproducibility between both exercises in also computed (see Table 28 on page 60 of the Final Report) and taken into account for the estimation of the pair-wise degrees of equivalence between participants in EUROMET.T-K3 and CCT-K3 (see Section 11.3 of the Final Report).

For each fixed-point temperature, the BIPM key comparison database displays the degrees of equivalence relative to the EUROMET reference value, and the pair-wise degrees of equivalence computed inside the EUROMET key comparison.

  • Linking EURAMET.T-K3.3, EURAMET.T-K3.1 and EURAMET.T-K3.5 to EUROMET.T-K3 and CCT-K3

The LACOMET results obtained in EURAMET.T-K3.3 are linked to the results of EUROMET.T-K3 and CCT-K3 using the participation of CEM in EUROMET.T-K3, whose results are linked to those of CCT-K3, as described above.
The BIM results obtained in EURAMET.T-K3.1 are linked to the results of EUROMET.T-K3 and CCT-K3 using the participation of VSL in EUROMET.T-K3.
The ROTH+CO.AG results obtained in EURAMET.T-K3.5 are linked to the results of EUROMET.T-K3 and CCT-K3 using the participation of VSL in EUROMET.T-K3.
This makes it possible to extend the EUROMET.T-K3 graphs of equivalence with LACOMET, BIM and ROTH+CO.AG results.
LACOMET and BIM degrees of equivalence relative to the CCT-K3 ARV are given on page 17 of the EURAMET.T-K3.3 Final Report and on pages 10 and 11 of the EURAMET.T-K3.1 Final Report, respectively.
The computation of ROTH+CO.AG degrees of equivalence relative to the CCT-K3 ARV is explained in Section 8.1 of the EURAMET.T-K3.5 Final Report.

print out

EUROMET.T-K3, EURAMET.T-K3.3, EURAMET.T-K3.1 and EURAMET.T-K3.5

NOMINAL TEMPERATURE : Tin Freezing Point, 505.078 K

  • Key comparison EUROMET.T-K3

For each fixed-point temperature, the difference (TR - TP) between the EUROMET reference value, TR, and TP, is computed as the weighted mean of all participants' results (Ti - TP), with weights inversely proportional to uiP, as explained in Section 8.1 of the Final Report.

For each fixed-point temperature, the degree of equivalence of laboratory i with respect to the EUROMET reference value is given by a pair of terms, both expressed in mK: Di = (Ti - TR), obtained from the differences relative to the Pilot Laboratory
Di = (Ti - TP) - (TR - TP), and Ui, its expanded uncertainty (k = 2), involving the measurement uncertainty at laboratory i, the uncertainty associated with the stability of the travelling SPRTs, and the repeatability of the calibration at the Pilot Laboratory (see Section 8.2 of the Final Report).
For each fixed-point temperature, the degree of equivalence between two laboratories i and j is given by a pair of terms, both expressed in mK: Dij = Di - Dj, and Uij, its expanded uncertainty at a 95 % level of confidence. The computation of Uij between participants in the same loop, and participants in different loops is explained in Sections 11.1 and 11.2 of the Final Report.
  • Linking EUROMET.T-K3 to CCT-K3

The Pilot Laboratory and the five Co-Pilots have participated in both comparisons.
The comparison of their averaged results in both exercises shows that they perform equally within 0.1 mK for all temperatures, except for the Zinc fixed-point temperature (0.23 mK) and the Tin fixed-point temperature (0.14 mK), as explained in Section 10.1 of the Final Report.
The uncertainty linked with the reproducibility between both exercises in also computed (see Table 28 on page 60 of the Final Report) and taken into account for the estimation of the pair-wise degrees of equivalence between participants in EUROMET.T-K3 and CCT-K3 (see Section 11.3 of the Final Report).

For each fixed-point temperature, the BIPM key comparison database displays the degrees of equivalence relative to the EUROMET reference value, and the pair-wise degrees of equivalence computed inside the EUROMET key comparison.

  • Linking EURAMET.T-K3.3, EURAMET.T-K3.1 and EURAMET.T-K3.5 to EUROMET.T-K3 and CCT-K3

The LACOMET results obtained in EURAMET.T-K3.3 are linked to the results of EUROMET.T-K3 and CCT-K3 using the participation of CEM in EUROMET.T-K3, whose results are linked to those of CCT-K3, as described above.
The BIM results obtained in EURAMET.T-K3.1 are linked to the results of EUROMET.T-K3 and CCT-K3 using the participation of VSL in EUROMET.T-K3.
The ROTH+CO.AG results obtained in EURAMET.T-K3.5 are linked to the results of EUROMET.T-K3 and CCT-K3 using the participation of VSL in EUROMET.T-K3.
This makes it possible to extend the EUROMET.T-K3 graphs of equivalence with LACOMET, BIM and ROTH+CO.AG results.
LACOMET and BIM degrees of equivalence relative to the CCT-K3 ARV are given on page 17 of the EURAMET.T-K3.3 Final Report and on pages 10 and 11 of the EURAMET.T-K3.1 Final Report, respectively.
The computation of ROTH+CO.AG degrees of equivalence relative to the CCT-K3 ARV is explained in Section 8.1 of the EURAMET.T-K3.5 Final Report.

print out

EUROMET.T-K3, EURAMET.T-K3.3, EURAMET.T-K3.1 and EURAMET.T-K3.5

NOMINAL TEMPERATURE : Zinc Freezing Point, 692.677 K

  • Key comparison EUROMET.T-K3

For each fixed-point temperature, the difference (TR - TP) between the EUROMET reference value, TR, and TP, is computed as the weighted mean of all participants' results (Ti - TP), with weights inversely proportional to uiP, as explained in Section 8.1 of the Final Report.

For each fixed-point temperature, the degree of equivalence of laboratory i with respect to the EUROMET reference value is given by a pair of terms, both expressed in mK: Di = (Ti - TR), obtained from the differences relative to the Pilot Laboratory
Di = (Ti - TP) - (TR - TP), and Ui, its expanded uncertainty (k = 2), involving the measurement uncertainty at laboratory i, the uncertainty associated with the stability of the travelling SPRTs, and the repeatability of the calibration at the Pilot Laboratory (see Section 8.2 of the Final Report).
For each fixed-point temperature, the degree of equivalence between two laboratories i and j is given by a pair of terms, both expressed in mK: Dij = Di - Dj, and Uij, its expanded uncertainty at a 95 % level of confidence. The computation of Uij between participants in the same loop, and participants in different loops is explained in Sections 11.1 and 11.2 of the Final Report.
  • Linking EUROMET.T-K3 to CCT-K3

The Pilot Laboratory and the five Co-Pilots have participated in both comparisons.
The comparison of their averaged results in both exercises shows that they perform equally within 0.1 mK for all temperatures, except for the Zinc fixed-point temperature (0.23 mK) and the Tin fixed-point temperature (0.14 mK), as explained in Section 10.1 of the Final Report.
The uncertainty linked with the reproducibility between both exercises in also computed (see Table 28 on page 60 of the Final Report) and taken into account for the estimation of the pair-wise degrees of equivalence between participants in EUROMET.T-K3 and CCT-K3 (see Section 11.3 of the Final Report).

For each fixed-point temperature, the BIPM key comparison database displays the degrees of equivalence relative to the EUROMET reference value, and the pair-wise degrees of equivalence computed inside the EUROMET key comparison.

  • Linking EURAMET.T-K3.3, EURAMET.T-K3.1 and EURAMET.T-K3.5 to EUROMET.T-K3 and CCT-K3

The LACOMET results obtained in EURAMET.T-K3.3 are linked to the results of EUROMET.T-K3 and CCT-K3 using the participation of CEM in EUROMET.T-K3, whose results are linked to those of CCT-K3, as described above.
The BIM results obtained in EURAMET.T-K3.1 are linked to the results of EUROMET.T-K3 and CCT-K3 using the participation of VSL in EUROMET.T-K3.
The ROTH+CO.AG results obtained in EURAMET.T-K3.5 are linked to the results of EUROMET.T-K3 and CCT-K3 using the participation of VSL in EUROMET.T-K3.
This makes it possible to extend the EUROMET.T-K3 graphs of equivalence with LACOMET, BIM and ROTH+CO.AG results.
LACOMET and BIM degrees of equivalence relative to the CCT-K3 ARV are given on page 17 of the EURAMET.T-K3.3 Final Report and on pages 10 and 11 of the EURAMET.T-K3.1 Final Report, respectively.
The computation of ROTH+CO.AG degrees of equivalence relative to the CCT-K3 ARV is explained in Section 8.1 of the EURAMET.T-K3.5 Final Report.

Comparison
Comparison close
Results
print out

EUROMET.T-K3, EURAMET.T-K3.3, EURAMET.T-K3.1 and EURAMET.T-K3.5

NOMINAL TEMPERATURE : Mercury Triple Point, 234.3156 K

  • Key comparison EUROMET.T-K3

MEASURAND : Resistance ratio, W, at fixed-point temperature
PILOT LABORATORY : LNE-INM

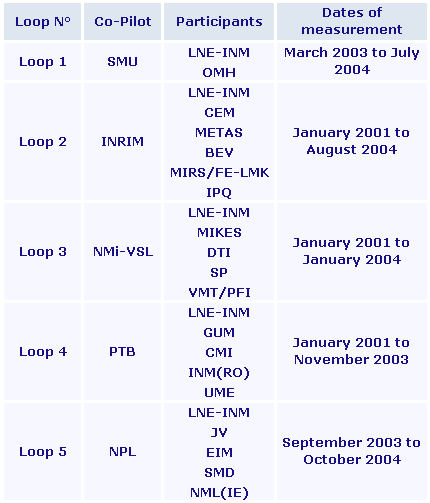
The key comparison EUROMET.T-K3 was carried out in five loops as described on Figure 1.1 on page 5 of the Final Report:

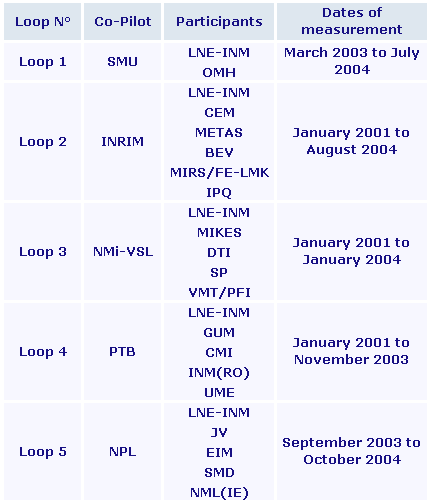
The individual laboratory measurements are given in Section 5 of the Final Report.
The temperature differences (Ti - TP) and associated standard uncertainties uiP are then deduced independently of the measurement loop. The indexes "i" and "P" refer respectively to laboratory i and to the Pilot Laboratory, and T to the temperature of a given fixed point.

  • Key comparison EURAMET.T-K3.3

Key comparison EURAMET.T-K3.3 is a bilateral comparison between CEM and LACOMET carried out in 2009

For the Mercury Triple Point, the temperature difference and corresponding expanded uncertainty (k = 2) are:
TLACOMET - TCEM = -0.10 mK and U(TLACOMET - TCEM) = 0.64 mK

  • Key comparison EURAMET.T-K3.1

Key comparison EURAMET.T-K3.1 is a bilateral comparison between BIM and VSL carried out in 2008-2009

For the Mercury Triple Point, the temperature difference and corresponding expanded uncertainty (k = 2) are:
TBIM - TVSL = -0.17 mK and U(TBIM - TVSL) = 0.49 mK

  • Key comparison EURAMET.T-K3.5

Key comparison EURAMET.T-K3.5 is a bilateral comparison between VSL and ROTH+CO.AG carried out in 2013

For the Mercury Triple Point, the temperature difference and corresponding expanded uncertainty (k = 2) are:
TROTH+CO.AG - TVSL = 0.38 mK and U(TROTH+CO.AG - TVSL) = 0.96 mK

print out

EUROMET.T-K3, EURAMET.T-K3.3, EURAMET.T-K3.1 and EURAMET.T-K3.5

NOMINAL TEMPERATURE : Gallium Melting Point, 302.9146 K

  • Key comparison EUROMET.T-K3

MEASURAND : Resistance ratio, W, at fixed-point temperature
PILOT LABORATORY : LNE-INM

The key comparison EUROMET.T-K3 was carried out in five loops as described on Figure 1.1 on page 5 of the Final Report:

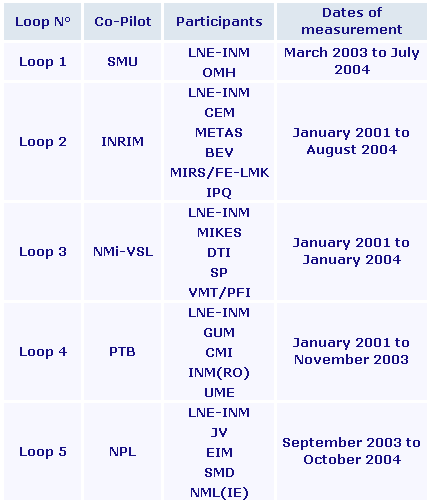
The individual laboratory measurements are given in Section 5 of the Final Report.
The temperature differences (Ti - TP) and associated standard uncertainties uiP are then deduced independently of the measurement loop. The indexes "i" and "P" refer respectively to laboratory i and to the Pilot Laboratory, and T to the temperature of a given fixed point.

  • Key comparison EURAMET.T-K3.3

Key comparison EURAMET.T-K3.3 is a bilateral comparison between CEM and LACOMET carried out in 2009

For the Gallium Melting Point, the temperature difference and corresponding expanded uncertainty (k = 2) are:
TLACOMET - TCEM = 0.26 mK and U(TLACOMET - TCEM) = 0.61 mK

  • Key comparison EURAMET.T-K3.1

Key comparison EURAMET.T-K3.1 is a bilateral comparison between BIM and VSL carried out in 2008-2009

For the Gallium Melting Point, the temperature difference and corresponding expanded uncertainty (k = 2) are:
TBIM - TVSL = 0.01 mK and U(TBIM - TVSL) = 0.52 mK

  • Key comparison EURAMET.T-K3.5

Key comparison EURAMET.T-K3.5 is a bilateral comparison between VSL and ROTH+CO.AG carried out in 2013

For the Gallium Melting Point, the temperature difference and corresponding expanded uncertainty (k = 2) are:
TROTH+CO.AG - TVSL = 0.78 mK and U(TROTH+CO.AG - TVSL) = 0.93 mK

print out

EUROMET.T-K3, EURAMET.T-K3.3, EURAMET.T-K3.1 and EURAMET.T-K3.5

NOMINAL TEMPERATURE : Indium Freezing Point, 429.7485 K

  • Key comparison EUROMET.T-K3

MEASURAND : Resistance ratio, W, at fixed-point temperature
PILOT LABORATORY : LNE-INM

The key comparison EUROMET.T-K3 was carried out in five loops as described on Figure 1.1 on page 5 of the Final Report:

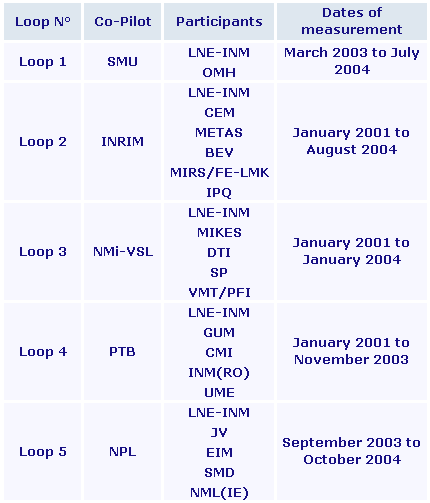
The individual laboratory measurements are given in Section 5 of the Final Report.
The temperature differences (Ti - TP) and associated standard uncertainties uiP are then deduced independently of the measurement loop. The indexes "i" and "P" refer respectively to laboratory i and to the Pilot Laboratory, and T to the temperature of a given fixed point.

  • Key comparison EURAMET.T-K3.3

Key comparison EURAMET.T-K3.3 is a bilateral comparison between CEM and LACOMET carried out in 2009

For the Indium Freezing Point, the temperature difference and corresponding expanded uncertainty (k = 2) are:
TLACOMET - TCEM = 0.4 mK and U(TLACOMET - TCEM) = 1.7 mK

  • Key comparison EURAMET.T-K3.1

Key comparison EURAMET.T-K3.1 is a bilateral comparison between BIM and VSL carried out in 2008-2009

For the Indium Freezing Point, the temperature difference and corresponding expanded uncertainty (k = 2) are:
TBIM - TVSL = 0.31 mK and U(TBIM - TVSL) = 0.90 mK

  • Key comparison EURAMET.T-K3.5

Key comparison EURAMET.T-K3.5 is a bilateral comparison between VSL and ROTH+CO.AG carried out in 2013

For the Indium Freezing Point, the temperature difference and corresponding expanded uncertainty (k = 2) are:
TROTH+CO.AG - TVSL = 1.47 mK and U(TROTH+CO.AG - TVSL) = 1.99 mK

print out

EUROMET.T-K3, EURAMET.T-K3.3, EURAMET.T-K3.1 and EURAMET.T-K3.5

NOMINAL TEMPERATURE : Tin Freezing Point, 505.078 K

  • Key comparison EUROMET.T-K3

MEASURAND : Resistance ratio, W, at fixed-point temperature
PILOT LABORATORY : LNE-INM

The key comparison EUROMET.T-K3 was carried out in five loops as described on Figure 1.1 on page 5 of the Final Report:

The individual laboratory measurements are given in Section 5 of the Final Report.
The temperature differences (Ti - TP) and associated standard uncertainties uiP are then deduced independently of the measurement loop. The indexes "i" and "P" refer respectively to laboratory i and to the Pilot Laboratory, and T to the temperature of a given fixed point.

  • Key comparison EURAMET.T-K3.3

Key comparison EURAMET.T-K3.3 is a bilateral comparison between CEM and LACOMET carried out in 2009

For the Tin Freezing Point, the temperature difference and corresponding expanded uncertainty (k = 2) are:
TLACOMET - TCEM = -1.3 mK and U(TLACOMET - TCEM) = 1.7 mK

  • Key comparison EURAMET.T-K3.1

Key comparison EURAMET.T-K3.1 is a bilateral comparison between BIM and VSL carried out in 2008-2009

For the Tin Freezing Point, the temperature difference and corresponding expanded uncertainty (k = 2) are:
TBIM - TVSL = -0.17 mK and U(TBIM - TVSL) = 1.0 mK

  • Key comparison EURAMET.T-K3.5

Key comparison EURAMET.T-K3.5 is a bilateral comparison between VSL and ROTH+CO.AG carried out in 2013

For the Tin Freezing Point, the temperature difference and corresponding expanded uncertainty (k = 2) are:
TROTH+CO.AG - TVSL = 0.65 mK and U(TROTH+CO.AG - TVSL) = 1.92 mK

print out

EUROMET.T-K3, EURAMET.T-K3.3, EURAMET.T-K3.1 and EURAMET.T-K3.5

NOMINAL TEMPERATURE : Zinc Freezing Point, 692.677 K

  • Key comparison EUROMET.T-K3

MEASURAND : Resistance ratio, W, at fixed-point temperature
PILOT LABORATORY : LNE-INM

The key comparison EUROMET.T-K3 was carried out in five loops as described on Figure 1.1 on page 5 of the Final Report:

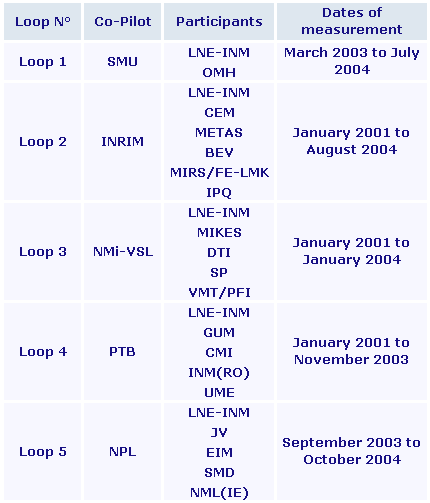
The individual laboratory measurements are given in Section 5 of the Final Report.
The temperature differences (Ti - TP) and associated standard uncertainties uiP are then deduced independently of the measurement loop. The indexes "i" and "P" refer respectively to laboratory i and to the Pilot Laboratory, and T to the temperature of a given fixed point.

  • Key comparison EURAMET.T-K3.3

Key comparison EURAMET.T-K3.3 is a bilateral comparison between CEM and LACOMET carried out in 2009

For the Zinc Freezing Point, the temperature difference and corresponding expanded uncertainty (k = 2) are:
TLACOMET - TCEM = -2.4 mK and U(TLACOMET - TCEM) = 2.1 mK

  • Key comparison EURAMET.T-K3.1

Key comparison EURAMET.T-K3.1 is a bilateral comparison between BIM and VSL carried out in 2008-2009

For the Zinc Freezing Point, the temperature difference and corresponding expanded uncertainty (k = 2) are:
TBIM - TVSL = -0.80 mK and U(TBIM - TVSL) = 1.6 mK

  • Key comparison EURAMET.T-K3.5

Key comparison EURAMET.T-K3.5 is a bilateral comparison between VSL and ROTH+CO.AG carried out in 2013

For the Zinc Freezing Point, the temperature difference and corresponding expanded uncertainty (k = 2) are:
TROTH+CO.AG - TVSL = 2.44 mK and U(TROTH+CO.AG - TVSL) = 2.33 mK